 Az első részben megismertük a keveréses kódokat, a mono-alfabetikus kódokat, valamint a homofonikus rejtjelezés alapjait. Épp ott tartottunk, hogy Etien Bazaires 1893-ban feltöri a homofonikus kódok királyát, a Grand Schiffet, amivel újabb hatalmas szöget ver be az egyábécés rejtjelezés sírjába.
Az első részben megismertük a keveréses kódokat, a mono-alfabetikus kódokat, valamint a homofonikus rejtjelezés alapjait. Épp ott tartottunk, hogy Etien Bazaires 1893-ban feltöri a homofonikus kódok királyát, a Grand Schiffet, amivel újabb hatalmas szöget ver be az egyábécés rejtjelezés sírjába.
Nomenklator táblák és kódkönyvek
Az addig kialakult helyzetet a rádió távíró feltalálása alaposan megváltoztatta. Ez ugyanis egyrészről drasztikusan felgyorsította a hírközlés sebességét és mennyiségét, másrészről mindennél fontosabbá tette a rejtjelezést. A homofonikus kódolás továbbfejlesztéseként egyre több szó kapott saját kódszámot (nomenklatort), így szép lassan a titkos üzenetben már csak számok szerepeltek; melyek komplett szavakat helyettesítettek. A kinyitáshoz pedig az addigi 2-5 oldalas clavis helyett már komplett kódkönyvre volt szükség (mint egy szótár).
Apropó, ha már könyveknél tartunk: a könyvnyomtatás kitalálása sokat segített az amatőr titkosítóknak: elég sok olyan rejtjelezési technika jelent meg, mely publikusan is elérhető szövegekre, általában könyvekre épült. A titkos üzenet hivatkozhatott a könyv egy betűjére, vagy egy szavára; s mivel ilyenekből bőven állt rendelkezésre, így homofonokat is lehetett használni. Optimális esetben ugyanaz a kódjel nem fordult elő kétszer a titkosított szövegben, így a megfejtés eléggé reménytelen volt.
Bár azért nem lehetetlen. A könyvkód egyik nagyon komoly hátránya ugyanis, hogy kódként használt könyv betűi és szavai nem véletlen sorrendben követik egymást (merthogy értelmes szövegről van szó). Így kellő környezettanulmányt végezve (szóba jöhető szövegek), és a valószínű szavak megsejtésével meg lehet tippelni a kódként használt könyv néhány szavát (ami egyben -ugye- az üzenet szava is). Ebből viszont már más szavak is megtippelhetők, és - jellegzetes szó esetén - akár a kódként használt könyvet is azonosítani lehet.
Egy jellegzetes példa a Beale-kód.
Ezt a 3 titkosított lapot tartalmazó szöveget 1820 körül egy Thomas Jefferson Beale nevű kalandor hagyta barátjánál, a szállodás Robert Morrissnál. Elment ugyanis egy kincskereső expedícióra; de megígérte, hogy visszatér. Ám mivel nem ő volt a Terminátor, így nem tért vissza. Egy idő után aztán Morriss megunta a várakozást, és egy haverjával együtt megpróbálta megfejteni a lapokat.
A három lapon csak számok szerepeltek, méghozzá elég nagy számok is:

Ez utóbbi tény arra utalt, hogy egy könyvkódról van szó - egy clavisban ugyanis nem szokott 1780 kódszimbólum lenni. Egy könyvben viszont simán van ennyi szó, még a rövidebbekben is.
A haver, egy bizonyos James B Ward rengeteg munka és némi szerencse árán rájött, hogy a második lap kódja a Függetlenségi Nyilatkozat. Így az olvashatóvá vált, és kiderült belőle, hogy egy elrejtett, 40 millió dolláros kincsről van szó. A helyét az első lap kódolja, a jogos tulajdonosokat a harmadik.
Sokan próbálták azóta is megfejteni ez a két lapot (főleg az elsőt…), de azóta sem sikerült senkinek rájönnie, hogy milyen könyv vagy szöveg nyitja őket. Vagy legalábbis nem kürtölte világgá.
A könyv-módszert amúgy hazánkban is használták, különböző szövegekkel. Például az 1848-as szabadságharc utáni Makk-Gaál-összeesküvés során népdalokat használtak "kódkönyvként".
A tetszőleges népdalt egy táblázatba másolták, a kód pedig numerikusan hivatkozott a sor/oszlopra. Tehát a betű helyett törtek álltak: 4/2, 16/3, stb. Nagyon büszkék voltak a módszerre, de valójában annyira azért nem volt jó: sima homofonikus rejtjelezés, ahol a kódtér a népdalokra korlátozódik.
Egy átlagember hány (bármilyen nyelvű) népdalt ismer..?
Amúgy az összeesküvés az 1848-49-es szabadságharc után szerveződött a Habsburg-uralom ellen, Makk ezredes vezetésével. Bukarestből irányították, de a székelyek voltak a leghatékonyabbak.
Az összeesküvés egyébként pont olyan volt, mint a rejtjelezési technikájuk: nagyon nép-nemzeti, nagyon romantikus, .... de nagyon átgondolatlan, óvatlan, és szervezetlen.
El is buktak. Talán egyszer lesz róluk poszt (kacsintok itt elsősorban '48-'49-es szakértőnkre...).
A könyvkód azon hibája, hogy a kódoló szöveg nem véletlenszerű amúgy korrigálható. Olyan könyvet kell készíteni, aminek az oldalai véletlen karakterekkel (vagy szavakkal) vannak tele, és ezt használni hivatkozási alapnak a titkosításnál.
Ilyen könyvvel működött sokáig az USA-USSR forródrót titkosítása is: minden üzenethez egy külön oldalt használtak fel a spéci kódkönyvből, és minden oldalt csak egyszer használtak. (Igaz, az kicsit más kódolás volt, de mindjárt ezt is elmesélem.)
Ez utóbbi trükk –az egyszer használatos kód- ezért is fontos, mert a kódkönyvek egyik nagy hibája pont az állandóság.
A kódkönyves titkosítás az első világháború környékén élte virágkorát. Az üzeneteket egy szótár-kódkönyv szerint számokká alakították, és az üzenet ezekből a számokból állt. Hogyan lehet feltörni?
Kódkönyv nélkül elég nehéz vele kezdeni bármit is, de nem reménytelen. Ugyanis a valószínű szó módszere itt is működik. A németek például pedáns emberek: leveleik elég formálisak, amiből sok minden kiderül. Aztán meg lehet figyelni, hogy az üzenet kinek megy, és az mit csinál a hatására. Ebből is ki lehet találni szavakat. Főleg több más üzenettel összehasonlítva. Aztán ott vannak a kódrendszer hibái: a szótárból kimaradt szavakat (jellemzően személyneveket) a számsor végére illesztették. Így egy kellően nagy szám nagy valószínűséggel egy újonnan színre lépett ember nevét takarja. Ebből előbb-utóbb kilogikázható, hogy ki a küldő.
Rettentően pepecs, lassú, és erőforrás-igényes munkáról van szó, de lehet vele eredményeket elérni. Mivel ugyanis a kódkönyvek lecserélése egy logisztikai rémálom, így aránylag ritkán cserélték őket. Magyarul: volt elég idő, és elég alapanyag rekonstruálgatni őket.
 Így fordulhatott elő, hogy amikor Arthur Zimmermann német külügyminiszter 1917. január 16.-án levelet küldött a mexikói kormánynak, akkor azt a brit titkosszolgálat elég nagy arányban meg tudta fejteni. Akkorra ugyanis már - rengeteg munka árán - rekonstruálták a német kódkönyveket.
Így fordulhatott elő, hogy amikor Arthur Zimmermann német külügyminiszter 1917. január 16.-án levelet küldött a mexikói kormánynak, akkor azt a brit titkosszolgálat elég nagy arányban meg tudta fejteni. Akkorra ugyanis már - rengeteg munka árán - rekonstruálták a német kódkönyveket.
A feltört táviratból kiderült, hogy az üzenet fontos. Zimmermann arra kérte benne Mexikót, hogy támadja meg az USA-t, és nyúljon le tőle pár államot. Így az USA nem Európával foglalkozott volna, cserébe Zimmermann német segítséget ígért Mexikónak. Ez akkor, abban a helyzetben egy teljesen khm. unortodox ötlet volt, de az angoloknak igencsak jól jött ez a "fecni". Ellenben nem adhatták át a félig feltört üzenetet az USA elnökének, mert ha az világgá kürtöli, akkor a németek rájönnek, hogy szivárog kódjuk. Lecserélik kódkönyveket, és az angolok bukják a feltörési képességüket.
Ezért inkább más megoldást kerestek. Amerikai titkosszolgálati segítséggel kerítettek egy korrupt tisztviselőt a mexikói német követségen, aki némi készpénzért átadta a desifrírozott változatot. Ez került aztán Woodrow Wilson elnökhöz, később az újságokhoz – óriási botrányt okozva.

Igazából az eset jól rávilágított arra, hogy most már valamilyen jobb módszer kell; ahol sokkal gyorsabban –akár naponta, sőt, üzenetenként- lehet kódot váltani.
De ehhez előbb vissza kell térnünk kicsit 1553-ba.
Poli-alfabetikus kódok
Ahogy már volt róla szó, a Caesar kódolással az a probléma, hogy a gyakoriság-analízis ellen védtelen. De arról is volt már szó, hogy a gyakoriság-analízis csak akkor működik, ha kellően hosszú az üzenet.
Ezen viszont elég egyszerűen lehet segíteni: az üzenetet fel kell szabdalni kellően kicsi darabokra, és azokat külön-külön kódolni más-más eltolási értékkel (kulccsal). Ezt a szabdalást úgy érdemes csinálni, hogy nehéz kegyen kitalálni, hogy mikor melyik Caesar kód használandó: praktikusan össze kell őket fésülni.
Ez az alapja a poli-alfabetikus kódoknak: nem EGY helyettesítéses kód van, hanem TÖBB egyetlen üzenetben.
A módszert sokan és sokszor újra fel- és feltalálták a történelemben, de elsőként Giovan Batista Belaso írta le 1553-ban. Ám később egy félreértés miatt Blaise de Vigenère nevét vette fel.
Az elv egyszerű, és a kódszón kívül csak egy ilyen egyszerű táblázat kell hozzá: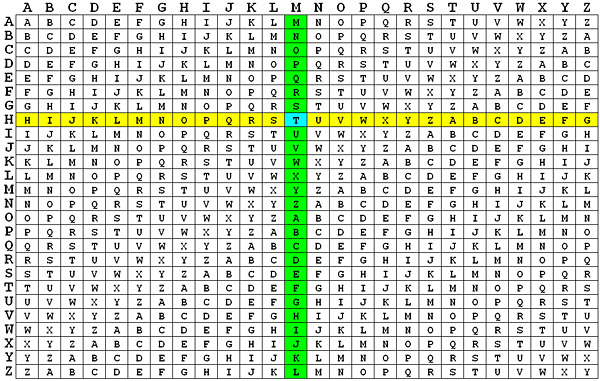
A használata gyerekjáték. Először is kell egy kódszó. Minél hosszabb, annál jobb.
Aztán fogjuk a kódszó első betűjét (mondjuk "H"), az adja meg a fenti táblázatban a sort, a titkosítandó üzenet első betűje pedig az oszlopot adja meg (mondjuk "M"). Így a táblázat megmondja, hogy "T", mint "Titkos" lesz a kódolt betű. Tulajdonképpen a kódszó betűje az eltolás mértékét adja meg, az oszlop pedig egy közönséges Caesar-kódoló.
Ezután fogjuk a kód második betűjét, és ez alapján cézárosítjuk az üzenet második betűjét. És így tovább. Ha a kód elfogy, akkor kezdjük elölről. Vigenère esetében 26 betűs kód volt, de ez bármennyi lehet.
Íme egy példa:
Kód: LEMIL
Szöveg: TITKOSITSUNK
Kód többször: LEMILLEMILLE
Szöveg még egyszer: TITKOSITSUNK
Titkosítva: EMFSZDMFAFYO
A módszer teljesen ellenáll a gyakoriság-analízisnek, de még a valószínű szó módszerének is – hisz ugyanazt a szót legközelebb más kódrészlet máshogy kódolja. Sokáig teljesen feltörhetetlennek tűnt a módszer, de mivel a kézi táblázatos keresgélés lassú és nehézkes művelet volt, csak a katonák használták időnként a nagyonszupertitkos üzenetek küldésére.
Ám 1848-ban, mikor egy Thwaites nevű fazon újra feltalálta a kódot és szabadalmaztatni akarta, Charles Babbage (jobbról) – a különc zseni – beszólt neki. Mire Thwaites kihívás elé állította: ha olyan nagy a szája, akkor törje fel a kódot.
Babbage foglalkozni is kezdett vele. A titkos üzenetet vizsgálgatva ismétléseket vett észre benne, ami abból fakadt, hogy ott véletlenül ugyanazt a karakterpárt ugyanaz a kód kódolta. Ebből viszont megtippelhető a kódszó hossza - legalábbis annak egész számú többszöröse. További vizsgálatokkal végül a kód hossza viszonylag pontosan meghatározható.
A kód hossza alapján viszont az üzenet szétbontható több, egyszerű Caesar-kódolt részre, ahol már működik a gyakoriság-analízis. Feltéve, hogy az üzenet elég hosszú, a kód meg elég rövid.
Babbage tehát feltörte a kódot, ám az eredményt nem publikálta. Állítólag a hadsereg nem örült volna neki, de lehet, hogy csak simán nem érdekelte tovább a kérdés.Így aztán 1863-ban a német kódfejtő, Friedrich Kasiski törte fel újra a Vigenère kódot. Ő egy olyan algoritmust alkotott, ami megmondja a kód hosszát, a többi meg már csak rutinmunka.
Mindemellett a Vigenère-rejtjelnek rengeteg további verziója született. Tulajdonképpen ilyen a Playfair módszer is, amely a kódszót egy táblázatba írja be, és a sor/oszlop azonosítókat betűpárként írja le. Közben néha lépteti a táblázatot.
De szintén Vigenère-klón például az Autoclave rendszer is, ami magát a titkosítandó szöveget használja fel - egy bizonyos eltolással - kulcsként. Az első pár karaktert egy kulcs-kulccsal titkosítjuk Vigenère-szerint, majd a későbbieket magával a szöveggel. Ez elsőre jó ötletnek tűnik, hisz így a kód hossza tulajdonképpen nagyobb, mint kódolandó szövegé (így a Kasiski-módszer elveszti az erejét, és a gyakorisági analízis is lehetetlenné válik). De másodikra megnézve már nem olyan jó a helyzet. Ugyanis ha az üzenet elejét feltörjük akár próbálgatásos módszerrel, akkor a többi már magától adódik – hisz maga az üzenet a kulcs.
Annyi azonban látszik: ha kód legalább olyan hosszú, mint a titkosítandó szöveg ÉS véletlen karakterekből áll, akkor a Vigenère-kód gyakorlatilag feltörhetetlen. És itt most hadd utaljak vissza az USA-USSR forródrótra.
A üzenet hosszával arányos hosszúságú (ál)véletlen kód viszont nem csak kódkönyvvel állítható elő, hanem algoritmikusan is. Kell egy álvéletlenszám-generátor, aminek ugyan sokféle kiindulási értéke lehet, ám egy adott indulási értékhez mindig pontosan ugyanazt a kódsorozatot generálja.
Ilyet leginkább géppel lehet csinálni, beköszöntött hát a kódoló-dekódoló gépek kora.
Titkosító gépek
A második világháborúra minden nagyhatalom rendelkezett titkosító gépekkel.
 A német Kryha, és az azonos elven működő a japán 91-shiki injiki (Red) és Angōki B-kata (Purple); a szintén német Rotor és az abból kifejlődött Enigma és Lorenz SZ40; az amerikai Hagelin és az orosz Crystal (amit -hogy úgy mondjam- a Hagelin B-211 “ihletett”); mind ugyanazt tudták akkoriban. Be lehetett gépelni a titkosítatlan üzenetet, és a gép az alapbeállításaitól függően kódolta az és visszaadta a titkosított szimbólumsort.
A német Kryha, és az azonos elven működő a japán 91-shiki injiki (Red) és Angōki B-kata (Purple); a szintén német Rotor és az abból kifejlődött Enigma és Lorenz SZ40; az amerikai Hagelin és az orosz Crystal (amit -hogy úgy mondjam- a Hagelin B-211 “ihletett”); mind ugyanazt tudták akkoriban. Be lehetett gépelni a titkosítatlan üzenetet, és a gép az alapbeállításaitól függően kódolta az és visszaadta a titkosított szimbólumsort.
A Kryha esetében két tárcsát használtak: az egyiken kellett kiválasztani a titkosítandó betűt, a másikon leolvasni a kódolt változatot. A két tárcsa együtt fogott, de mikor megnyomtak a gépen egy gombot, akkor a tárcsák egymáshoz képest valamennyivel (látszólag véletlenszerűen) elfordultak. Egy trükkös fogazatú fogaskerék-mechanika gondoskodott az álvéletlenségről. Tehát tulajdonképpen egy mechanikus Vigenère-kódolóról van szó, melynek kulcsa a belső fogaskerék fogazásában (és kialakításában) ölt testet.
Ugyanezen az elven működött a japán Red, majd az abból kifejlesztett Purple gép is (a nyitóképen látható): ez is a rotoros kódolók családjába tartozott. Csak persze sokkal bonyolultabb volt: az elektromechanikus szerkezetben forgó rotorok és jelfogók kódolták át a bejövő üzenetet. Minden karakter kódolása után a rotorok léptek egyet, és az új villamos összeköttetések miatt a következő karaktert már máshogy kódolta a gép. Emellett kézi, dugaszolós/kapcsolós keverés is volt benne. A kezelő egy billentyűzeten át gépelte be az üzenetet, aminek titkosítása után az eredményt egy villanyírógép köpte ki. (A szőrös villák el is kerülték a gépet messzire.) A gép nagyon bonyolult volt: 4 rotor, 70 billió féle kapcsoló-beállítás - emiatt a japánok a háború végéig feltörhetetlennek tartották.
Adódik a kérdés: akkor mégis hogy törték fel?
Hát először is: ki kellett deríteni, hogy mi van benne, hogyan működik. A Purple esetében az üzenetváltás gyengeségeit használták ki a megértéséhez, tehát a gép gyenge pontja a használat módjában volt. Mivel nem volt sorozatgyártásban, így kevés volt belőle. Ezért eleinte elég ritkán használták és sok üzenetet az akkor már feltört elődgépen, a Red-en is átküldtek. Így ugyan csak viszonylag kevés üzenet állt rendelkezésre a feltöréshez, ám ezeknek megvolt a titkos és a nyitott változata is. További hiba volt a magánhangzók külön kódolása a telexes átvitel egyszerűsítésére. Így a kódfejtők - 18 hónapi munka után - matematikailag modellezni tudták a gépet, ami alapján tudtak építeni egy replikát.
Ez még persze kevés, az üzenetek kibontásához tudni kellett a napi kódot is. Ezért ezt kezdték intenzíven tanulmányozni. Amikor az amerikaiak rájöttek, hogy a japánok hibásan generálják a napi kulcsot (ugyanis minták és ismétlődések voltak benne), akkor megpecsételődött a gép sorsa. Pedig a Purple a korszak legbonyolultabb és legjobb gépe volt. Fegyelmezett használattal és jó kulcsgenerálással tényleg beletörhetett volna a szövetségesek bicskája - ami miatt - például - a Midway-csata máshogy alakult volna.
Jól mutatja az eset, hogy:
1. Nem lehet nagyképűnek lenni, és azt gondolni, hogy tökéletes titkosítást alkottunk.
2. A rejtjelezés olyan, mint a lánc: az erősségét a leggyengébb láncszem ereje adja meg. Ha ez a használat módja, akkor mit sem ér a szuper technika.
Az amerikaiak rejtjelező gépeit nem tudták feltörni a háború folyamán, pedig messze nem voltak olyan jók, mint a Purple. Ám ők nagyon tudatosan és fegyelmezetten használták.
A leghíresebb kódológép viszont vitathatatlanul a német Enigma volt. Ez is hasonló elven működött: forgó gumitárcsák voltak benne, melyek a két oldalukon lévő érintkezőket keverve kötötték össze.

Így a billentyűzetről – vagy az előző korongról - érkező betűt egy másik betűvé konvertálta (strukturális okok miatt sosem kódolta a betűt saját magára, ami egy kihasználható hiba volt a feltörésekor). A kereskedelmi Enigmában 3 korong volt sorba kötve, és ezek minden karakter leütése után fordultak egyet. Volt még hozzá egy kézi keverő, és egy jelfordító – ami még egyszer átküldte a villamos jeleket a keverőtárcsákon. A végén egy lámpa kigyulladása jelezte, hogy mire konvertálta a betűt a gép.
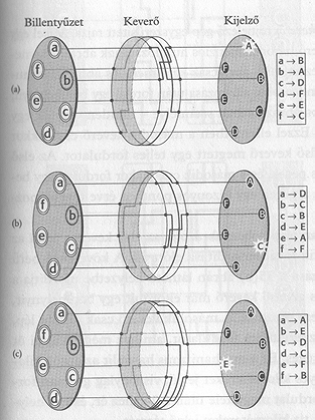
A tárcsák sorrendje és kiinduló helyzete, valamint a kézi keverő együttesen adták meg a üzenet kódját, amit a németek naponta változtattak. Egy 3 tárcsás gépen 17576 tárcsakód volt beállítható (mindösszesen 10000000000000000 kódverzió létezett).
 A német Enigmát kicsit máshogy törték fel, mint a Purple-t. Ugyanis nem kilogikázták a működését, hanem a francia titkosszolgálat 1931-ben egyszerűen megvásárolta egy kémtől a kapcsolási- és működési rajzát. Így tudtak replikát építeni, ám a napi kódokkal már nem tudtak megbirkózni. Feladták, így a - németekre gyanakvóan tekintgető - lengyelek vették át a stafétabotot a tehetséges ifjú matematikus, Marian Rejewski vezetésével.
A német Enigmát kicsit máshogy törték fel, mint a Purple-t. Ugyanis nem kilogikázták a működését, hanem a francia titkosszolgálat 1931-ben egyszerűen megvásárolta egy kémtől a kapcsolási- és működési rajzát. Így tudtak replikát építeni, ám a napi kódokkal már nem tudtak megbirkózni. Feladták, így a - németekre gyanakvóan tekintgető - lengyelek vették át a stafétabotot a tehetséges ifjú matematikus, Marian Rejewski vezetésével.
Kiderült, hogy a németeknél nem csak naponta változó (napi) kód volt, de –mivel még ez is túl sok kimenő üzenetet jelentett volna egyetlen kóddal – üzenet-kódot is használtak (~véletlenszerűen változtattak a keverőtárcsa-beállításokon, miközben minden más maradt). Ezeket a kódokat a napi kóddal titkosítva küldték el az üzenetek előtt, mégpedig kétszer - a hibaarány csökkentése miatt.
Ez pedig hiba volt, amire már alapozni lehetett. A teljes kódtér (matematikai) csökkentése után Rejewsky vezetésével építetek egy 6 Enigmából álló kódtörő gépet, ami szépen végigpróbálgatta az összes maradék lehetőséget, és így meghatározta a napi kódot. Ebből meg adódott az üzenetkód. A feltörő gépet a jellegzetes kegyegő hangja miatt „bombának” hívták. Remekül működött, így 1933-tól már rutinszerűen olvasták a német enigmás üzenetváltást (a képen már a Turing-féle 12 Enigmás „Bomba+” látható).
 A németek 1938-ban 3-ról 5-re növelték a kódtárcsák számát, törölték a dupla küldés szabályát, és egy sor további előírást is bevezettek a kódtörés akadályozására. Valamint 1939-ben lerohanták Lengyelországot, így a munkát ettől kezdve a Bletchley Park szakemberi folytatták.
A németek 1938-ban 3-ról 5-re növelték a kódtárcsák számát, törölték a dupla küldés szabályát, és egy sor további előírást is bevezettek a kódtörés akadályozására. Valamint 1939-ben lerohanták Lengyelországot, így a munkát ettől kezdve a Bletchley Park szakemberi folytatták.
Egy csomó mindent elölről kellett kezdeni, és innentől a "bomba" teljesítménye sem volt már elegendő.
Ellenben a német precizitásra továbbra is lehetett számítani: a minden nap 6:00-kor sugárzott időjárás-jelentés jó alap volt a valószínű szó módszerhez. Aztán rájöttek, hogy sok német rádiós gyenge üzenetkulcsot használ (mindig ugyanazt, vagy túl egyszerűt). Ráadásul a szigorúnak tűnő előírás, miszerint minden nap minden keverőtárcsát át kell tenni máshová ÉS minden keverő-beállítást is módosítani kellett, bizony többet ártott, mint használt: csökkentette a kulcsteret.
Házi feladat: 3 tárcsa esetén mennyit csökkent a kipróbálandó variációk számán, ha a már feltört előző napi kódhoz képest egyetlen tárcsa sem maradhat a helyén az új napi kódban?
 Az akkor már híres matematikus és főállású zseni, Alan Turing (balról) tökéletesítette a „bombát” (többek között), így a németek már hiába fejlesztették rendületlenül tovább a rendszert; már mindegy volt. Így a kódtörők figyelme a másik német gép, a Lorenz SZ40 felé fordult (itt jobb alul). Ide viszont egy új kódtörő eszköz kifejlesztése kellett.
Az akkor már híres matematikus és főállású zseni, Alan Turing (balról) tökéletesítette a „bombát” (többek között), így a németek már hiába fejlesztették rendületlenül tovább a rendszert; már mindegy volt. Így a kódtörők figyelme a másik német gép, a Lorenz SZ40 felé fordult (itt jobb alul). Ide viszont egy új kódtörő eszköz kifejlesztése kellett.

Ezt a gépet csak a nagyon-nagyon fontos, jellemzően Hitler által írt üzenetek titkosítására használták. A 12 tárcsás gép sokkal erősebb titkosító automata volt, mint az Enigma. Feltörhető volt ugyan, de túl komplex volt a meglévő „bombáknak”. A feltörés így nagyon sok kézi munkát igényelt, ami lelassította az üzenetek megfejtését. Ezért Max Newman és Alan Turing úgy gondolták, hogy egy programozható elektronikus gépet kéne rá építeni. Ez lett 1943-ban a Colossus, a világ első programozható elektronikus számítógépe, ami az addigi 6 hetes feltörési időt pár órára csökkentette.
A Colossus szigorúan titkos volt. Két verziója épült Tommy Flowers főmérnök vezetésével, a második (1944) jóval fejlettebb volt. Alapvetően egyszerű logikai műveletekre volt képes, de arra programozhatóan. Alapvetően relékből, forgó mechanikus rotorokból és -főleg- rádiócsöves áramkörökből épült fel. RAM nem volt benne, az utasításokat lyukszalagról olvasta. Így is meglehetősen gyorsan hajtotta végre az 5 biten kódolt utasításokat..
Összesen 10 gép épült a háború végéig, ám akkor mindet megsemmisítették, és a terveket is titkosították. Így az „Első Elektronikus Számítógép” címet az ENIAC vehette át 1946-ban. (A képen egy Colossus Mark II. változat.)
Produkciós titkosítások
Ugyan még sok éven át készültek elektromechanikus – később egyre inkább elektronikus- kódoló gépek, de a számítógépek megjelenése nagyon új irányba terelte a titkosítás történetét. Ugyanis:
- A számítógépek nem szöveget akarnak titkosítani, hanem bitfolyamot (ami persze reprezentálhat szöveget, de bármi mást is)
- Számítógépe mindenkinek lehet, tehát egyre kevésbé katonai és diplomáciai territórium a rejtjelezés.
- A számítógépek megjelenése gyorsan túl kicsivé tette a hagyományos titkosítások kódterét. Egyszerűen pillanatok alatt végig lehet próbálgatni az összes változatot. Míg a történelem során mindig az egyszerűen használható, de mégis "feltörhetetlen" kód kifejlesztése volt a cél, addig innentől kezdve már a komplex, ám „kellően nehéz feltörni”-kóddal is elégedettek lehetünk.
- Míg a középkorban – de még az újkorban is - a rejtjelek feltörését irodalmárok, nyelvészek végezték, addig a XX. század közepétől már a matematikusoké a terep.
- A kulcsok kiosztása sarkalatos jelentőségűvé vált.
A korszerű követelményeknek megfelelő titkosítási algoritmusok egyik úttörője a Lucifer-kódolás volt.
A Lucifer nem akart feltörhetetlen lenni: egyszerűen csak egy egyszerűen megvalósítható, gyors, szimmetrikus kódolást akart megvalósítani. Olyat, ami az akkori (1976-77-es technikai színvonalon) igen nehezen törhető.
Az elv itt egyszerű: végy egy olyan matematikai műveletet, mely 64 bites csomagokon működik 56 bites kulccsal, egyszerű megvalósítani, és ismételve nem összevonható („nem csoport”). Azaz ha többször elvégezzük egymás után, akkor ezek a lépések nem helyettesíthetőek egyetlen művelettel. Így az önmagukban egyszerű és gyenge lépések ereje összeadódva egy kellően komplex kódot ad.
 Sikerült is találni egy módszert, amit 16-szor ismételve egymás után már megfelelő hatásfokú volt a titkosítás (lásd még: lavina-effektus: egyetlen bit eltérés teljesen más eredményre vezet.). Ezt kiegészítették még némi bitkeveréssel, hibavédelemmel és miegymással, és kész is volt a Lucifer.
Sikerült is találni egy módszert, amit 16-szor ismételve egymás után már megfelelő hatásfokú volt a titkosítás (lásd még: lavina-effektus: egyetlen bit eltérés teljesen más eredményre vezet.). Ezt kiegészítették még némi bitkeveréssel, hibavédelemmel és miegymással, és kész is volt a Lucifer.
A 64 bites (56+hibavédelem) kulcsot használó módszer DES (Data Encryption Standard) néven vált szabványossá. Hardverben egyszerűen megvalósítható módszer volt, amit gyorsasága és egyszerűsége miatt sokan megkedveltek. Ám egy idő után az 56 bites névtér kicsinek bizonyult. Ezen segítendő egymás után háromszor végezték el a titkosítást (3DES, TripleDES), de ez is csak az idő húzására volt elég: ma egy átlagos PC percek alatt feltöri a kódot.
(Ennek ellenére ma is sokszor használják a 3DES-t, kevésbé kritikus helyeken.)
A fenti képen amúgy egy áramköri kártya látható, mely a Electronic Frontier Foundation által 1998-ban gyártott Deep Crack része volt. Ezt a 250 ezer dolláros gépet a DES feltörésére alkották, és 96 nap alatt teljesítette is a kihívást. Később már 22 óra alatt is ment a dolog, a technika meg azóta sokat fejlődött...
A DES helyett tehát új titkosítási szabvány kellett, ahol a győztes a Rijndael algoritmus (helyettesítéses + lineáris transzformációs kódolás) 128-256 bites kóddal üzemelő változata lett. Ezt 2000 októbere óta AES (Advanced Encryption Standard) kódként ismerjük.
Egy másik, hasonló eljárás az IDEA (International Data Encryption Algorithm), ami egy hasonló elvű, de 128 bites kulccsal működő titkosítás. Ezt használja az otthoni titkosításra kitalált PGP (Pretty Good Privacy) szabvány v2.0 változata is. Még nem találtak rajta fogást.
A szimmetrikus kulcsú titkosításnál a titkosító és a felnyitó is ugyanazt a kulcsot használja. Ehhez viszont előbb meg kell állapodniuk a kulcsban, ami minden eddig tárgyalt titkosítási eljárásnál problémát jelent. Ha a középkorban az egyik fél clavist küldött a másiknak, akkor mindig fennállt a lehetősége, hogy azt útközben lemásolta valaki. Az első világháborús kódkönyveket is el lehetett lopni, ami jellegénél fogva alkalmas titkosításra és felnyitásra is. A Purple vesztét is a kódok kiosztásának hibája okozta. Szóval régi probléma ez, ami az 1960-as évek környékén már nagyon akadályozta a titkosítás üzleti elterjedését.
Amúgy van arra megoldás, hogy kulcsot küldjünk nem biztonságos átviteli csatornán. Tegyük fel, hogy Alice küldani akar Bobnak egy clavist. Beteszi egy dobozba, és azt lelakatolja. Csak neki van a lakathoz kulcsa. Elküldi a dobozt Bobnak, de ő nem tudja kinyitni. Ám nem is akarja: ráteszi a saját lakatját, amihez már csak neki van kulcsa. Ezután a dobozt visszaküldi Alice-nak, hogy az vegye le a saját lakatját és küldje el neki újra. Így a clavis átér, miközben minden lépésnél lakat védte.
A módszer működik, de közben a titkos clavis háromszor ment át a veszélyes csatornán, és ha Alice vagy Bob lakatja nem elég erős, akkor már bukik is a kulcs-csere. Ráadásul a “lakat” olyan kód lehet csak, amit egymástól függetlenül lehet mindkét oldalról feltenni és levenni. Ilyen például a Caesar-kód….
Ezen a problémán töprengett Whitfield Diffie is az ArpaNet kapcsán a 60-as években. Azt találta ki, hogy olyan titkosítás kell, aminek két külön kulcsa van: az egyik csak titkosításra, a másik csak kinyitásra jó. Ez az aszimmetrikus kulcsú titkosítás, ami megoldja a kulcsok problémáját. Ám megcsinálni már nem olyan egyszerű feladat: olyan matematikai művelet kell hozzá, ami egyik irányban egyszerűen elvégezhető, de visszafelé már nem.
Végül a megoldás Ron Rivest, Adi Shamir és Leonard Adleman neveihez fűződik (R.S.A.). Ők a maradék-osztásra és a prímtényezős felbontásra építették módszerüket.
Lássuk csak: mennyi 12874675318267 szorozva 157856746827-tel? Egyszerű: számológép beizzít, 30 másodperc sem kell hozzá; itt a megoldás: 2032354362195499467388809. Könnyű. Mármint egy számítógépnek. Na de fordítva is megy? Lássuk csak: melyik két szám szorzata ez?
114381625757888867669235779976146612010218296721242362562561842935245733897830597123563958705058989075147599290026879543541
Ezt a feladatot Martin Gardner adta fel 1977-ben. 1994-re sikerült is egy 600 fős csapatnak megoldania. Szóval ez már nem olyan triviális feladat, mint egy sima szorzás. Odafelé jól megy, visszafelé nehéz. Pont ez kellett az RSA-hoz.
A dolgot súlyosan leegyszerűsítve így működik:
Két kulcs van: az egyik csak titkosítani tud, és ként nagy szám szorzata. Ez a szorzat a nyilvános kulcs, amivel csak titkosítani lehet. A kibontáshoz viszont csak olyan képlet áll rendelkezésre, melyhez kell az eredeti két szám is. Ez a titkos kulcs. Tehát küldeni mindenki tud üzenetet, csak elolvasni nem. Kibontani csak a címzett tudja, mivel ő ismeri az eredeti szorzókat is.
Bob tehát nyilvánosan publikálja a saját nyílt kulcsát. Mikor Alice küldeni akar neki egy üzenetet, ezt a nyílt kulcsot használva titkosít, majd a titkos üzenetet küldi Bobnak. Senki sem tudja azt visszafejteni, csak Bob. Nincs tehát kulcselosztási probléma, mindenki boldog.
Illetve csak majdnem: ott van például a hitelesítés kérdése: ki küldte az üzenetet? Nem hamis?
Erre is jó a módszer, csak fordítva kell alkalmazni. Ez a digitális aláírás.
 Meg ott van az a gond, hogy az RSA képletei kicsit számítás-igényesek. Így például a titkos webes kapcsolatoknál használt SSL-módszer első verziói is csak a közös kulcs megbeszéléséhez használták, utána már a DES dolgozott.
Meg ott van az a gond, hogy az RSA képletei kicsit számítás-igényesek. Így például a titkos webes kapcsolatoknál használt SSL-módszer első verziói is csak a közös kulcs megbeszéléséhez használták, utána már a DES dolgozott.
Azt hiszem, hogy az eddigiekből is jól látszik: a modern kori titkosítás rengeteg matematikáról és még több mágikus 3 betűs mozaikszóról szól. Ez már nagyon messze vezet az eredeti célomtól, így itt most abbahagyom a történetet. Aki érzi magát elég kockának a folytatáshoz, az úgyis megtalálja hozzá a forrásokat.
Akiben viszont sikerült felkelteni az érdeklődést a klasszikus titkosírások iránt azoknak ajánlom Láng Benedek egészen kitűnő blogját: http://kripto.blog.hu, esetleg a Kódfejtő blogot: http://kodblog.blog.hu, vagy ezek társoldalait. Rengeteg régi titkosírás várja még a kódtörőket, úgyhogy sok sikert!
-
A képeket a netről szereztem.
Felhasznált irodalom:
1. http://hu.wikipedia.org/wiki/A_kriptográfia_története és további Wiki oldalak.
2. http://www.hit.bme.hu/~buttyan/courses/Revkomarom/crypto_history.pdf
3. http://kripto.blog.hu és rengeteg posztja.
4. http://109.74.55.19/tananyagok/tananyagok/rendszergazda/Rendszer_es_Adatvedelem.pdf
5. www.eotvos-tata.sulinet.hu/kollegium/NTP/titkosiras.ppt
7. www.inf.u-szeged.hu/~zlnemeth/crypto/crypt1.pdf
8. https://sites.google.com/site/balazsrozalia/home/szimblumok/meghkkent-titkosrsok








2015.01.27. 08:38:21
Az Enigmával kapcsolatban én úgy tudtam, hogy az első verziót a lengyel titkosszolgálat szereztem meg. És volt a németeknek a háború alatt egy meteorológiai állomásuk a sarkkörnél, amit a szövetségesek békén hagytak, csak a háború végén szóltak nekik. Ezek az üzenetek ugyanis nagyon sablonosak és kódolva küldték, így a váltások feltörését nagyban segítette.
Titus Pullo Urbino 2015.01.27. 09:11:18
Az Enigma feltörésének dicsőségét a lengyelek maguknak követelik, ugyanúgy, ahogyan az angolok is. Ki tudja, melyik volt a döntő momentum?
A Lucifert pedig jó volt olvasni, nem sokat hallottam még eddig róla, nekem ze eddig kiesett.
Köszönjük PZS!
Zig Zag · http://lemil.blog.hu/ 2015.01.27. 10:24:29
nandras01 2015.01.27. 12:39:38
molnibalage · https://militavia.blog.hu/ 2015.01.27. 13:32:33
Papírzsepi · http://lemil.blog.hu 2015.01.27. 13:43:00
Fredddy 2015.01.27. 13:52:11
Papírzsepi · http://lemil.blog.hu 2015.01.27. 14:13:38
Amúgy az is kérdés, hogy:
1. Lehet-e a vizsgálandó teret szűkíteni, kihasználva a módszer valamilyen gyengeségét
2. Lehet-e a kódtörő algoritmust a kódtörő gépre optimalizálni. Például a videokártyák nagyon erősek mátrix-műveletek elvégzésében. Ha sikerül a feladatot ilyen műveletekre optimalizálni ÉS párhuzamosítani, akkor nagyon meggyorsítható a kódtörés.
Szóval a dolog messzire vezet, és sajnos kifelé a Lemil hatóköréből.
2015.01.27. 14:14:19
Fredddy 2015.01.27. 14:49:23
@Hadrian77: alapvetően igen, de a számítástechnika fejlődését figyelembe véve ezt az időt érdemes elég nagy rátartással meghatározni.
2015.01.27. 15:04:08
koalakotro 2015.01.27. 15:16:48
A modern eljárásokhoz azonban tennék néhány kiegészítést.
A 3DES-t a mai számítógépek sem tudják percek alatt feltörni, ott a "névtér" 112 bites és különböző szervezetek akár 2030-ig is biztonságosnak tartják. A legjobb példa arra, hogy még ma is viszonylag biztonságosnak tekinthető az az, hogy a chipes bankkártyák is ezt használják (EMV, ha valaki többet szeretne tudni). Más kérdés, hogy az AES biztonságosabb, és, ami talán még fontosabb, lényegesen gyorsabb, így nem érdemes új rendszert tervezni 3DES-sel.
Egy ilyen jellegű posztban szerintem felesleges megemlíteni az IDEA-t, mert szinte sehol sem használják, a PGP-t sem használják már sokan (lemeztitkosításra legalábbis). Ilyen célokra AES-től eltérő kódolást ritkán látni.
koalakotro 2015.01.27. 15:21:21
Amennyiben 256-bites a kulcstér, úgy még ideális esetben is (1 kulcs kipróbálása egyetlen energia kvantum) több energiára lenne szükség a feltöréshez, mint amennyit a Nap sugároz az élettartama alatt. Ezt nevezik termodinamikai korlátnak.
A gráf bejárása nem NP-teljes probléma. Az ideális útvonal keresése sem NP-teljes probléma, annyira nem az, hogy Dijkstra algoritmusa komplexitása a csúcsok számával négyzetesen nő.
koalakotro 2015.01.27. 15:29:02
Hmm, ezt átolvashattam volna :)
Szóval gráfokban legrövidebb útvonal megtalálására létezik olyan algoritmus (például Dijsktra algoritmusa), amelynek futási ideje a csúcsok számával négyzetesen aránylik.
Az útvonaltervezésben szerencsére nem nehéz elméleti szempontból.
Titus Pullo Urbino 2015.01.27. 15:31:27
koalakotro 2015.01.27. 15:33:48
A dolog lényege, hogy van egy titkos kulcs, ami megvan a szerveren meg a telefonodon is, és ehhez mindig hozzáadják az aktuális idő fél percre kerekítve. Ezután az egészből készítenek egy úgynevezett hash-t, amit nem tárgyalt a bejegyzés, de röviden annyi a dolog lényege, ebből csak nagy munka árán lehet vissza állítani az eredeti adatot (titkos kulcs + idő). Lényegében a hash az, amit te begépelsz.
Sajnos nekem kevésbé jó írói képességeim vannak, mint a poszt írójának, de remélem, azért érthető. :)
Fredddy 2015.01.27. 15:36:31
koalakotro 2015.01.27. 15:39:04
Van egy úthálózatunk, ahol eljuthatunk 10 városba. Itt mondjuk két város közötti útvonalat megtaláljuk 100 másodperc alatt.
Ha egy újabb várost bekapcsolunk az úthálózatba, akkor viszont 121 másodpercre nő a számítási idő. (10^2 = 100, 11^2 = 121)
Ha ez egy NP-teljes probléma lenne, akkor egyetlen város hozzáadásával megduplázodna a számítási igény, vagyis 11 városra már 20 másodpercet kellene számolni.
Fredddy 2015.01.27. 15:42:30
*Dízel teherkocsival, na, de értitek :)
tudi 2015.01.27. 17:12:31
haku 2015.01.27. 18:47:42
Az italautomatás problémát pedig úgy hívják, hogy "utazó ügynök probléma" (en.wikipedia.org/wiki/Travelling_salesman_problem). NP-teljes (azaz a bemenet növelésével (városok száma) a számítási idő exponenciálisan nő.)
Kicsit OFF, valamint nem kissé KONTEÓ is: A quantum számítógép elméletileg P időben (=erős géppel belátható időn belül) futtat NP teljes problémákat (kihasználja, hogy egyszerre több állapotban is lehet.) Ezzel RSA-kat feltörni elméletileg már értelmes futási idővel lehet. Kíváncsi lennék vajon nem rejtegetnek efféle célra quantum szmámítógépeket mindenféle sivatagi bázisokon :).
Mindenestre a quantum számítógépek megjelenése alapjában fogja felforgatni a titkosítások világát.
Papírzsepi · http://lemil.blog.hu 2015.01.27. 19:14:33
Minden esetre a tapasztalatom szerint a hadsereg általában jópár évvel előbbre tart a fejlesztésekkel, mint a kereskedelmi cégek. Azok meg pár évvel előzik az egyetemeket...
Ha most a Google kísérletezik vele, akkor katonáéknak már lehet használható is.
Megjegyzem a kvantumszámítógéphez kvantumtitkosítás is jár, amit jelenleg nem lehet sem feltörni, nem lehallgatni.
Szóval sima generációváltásról van szó, az erőviszonyok nem változnak....
koalakotro 2015.01.27. 20:33:41
Előnye viszont, hogy a módszer nem csak jelenleg feltörhetetlen, hanem valóban az, hacsak ki nem derül, hogy máshogy működik a fizika. Ilyen rendszereket egyszerűen máshogy kell megtámadni, a kikerült NSA dokumentumok alapján nem kell félteni a fiúkat-lányokat, elég találékonyak ilyen téren, megoldják.
A kvantumszámítógépekkel az a baj, hogy jelenleg nincsenek (publikusan elérhető) algoritmusok, amelyek biztonságosak maradnak az eljövetelükkel is. Ha tényleg tudnak ilyet építeni és használni kódtörésre, akkor az nagyon megrázná a világot. Például a bankrendszer eléggé épít ezekre a technológiákra. De jelenleg ez még inkább a konteók témakörébe tartozik, szerencsére.
Minorkavidor 2015.01.27. 20:35:45
Az Enigma története nem Németországban, hanem Hollandiában. 1919-ben, a delfi Hugo Alexander Koch szabadalmaztatja „titkosító gépét”, a szabadalom száma: 10 700. a gép kudarc, mind használati, mind kereskedelmi szempontból. 1923-ban mégis megvásárolja szabadalmát a Berlinben született mérnök, Dr. Arthur Scherbius. Még ebben az évben használhatóvá teszi és átkereszteli, a görög enigma (m: titok) nevet kapja. A Scherbius által alapított Chiffrienmaschiren AG Berlinben, a Steglitter Str.2. alatt kezdi meg a termelést 1923 júliusában. A gépet kereskedelmi forgalomba, vállalkozások üzleti levelezéseinek kódolására szánják. A gép a közönséges villanyírógép nehezebb változatának tűnt. A billentyűzet elektromos leütésre elektromos impulzusokat visz át a tekercselt kódoló hengerekre. Minden henger belső felületén 26 elektromos érintkező van, melyek megfelelnek az ABC betűinek. Scherbius melle dagad a büszkeségtől. „Ha egy ember éjjel-nappal szünet nélkül dolgozna és minden percben másik kódot próbálna ki, 42 000 évre volna szüksége, hogy minden kombinációs lehetőségen végig menjen”, e szlogennel reklámozta a gépet.
Az A és B modell előbb Berlinben debütál, majd bemutatkozik a Lipcsei Vásáron. 1924 augusztusában, a stockholmi postás-világkongresszuson mutatják be a nagyérdeműnek. A cég külföldön is értékesít: Nagy-Britanniába, Japánba, Lengyelországba, az USA-ba, Svájcba és Svédországba is szállítanak a „kedves vevőknek” vagy ott is szabadalmaztatták a gépet ). a gép már használható, de Scherbius haláláig mégsem kaszált. Halála után, 1934-ben, a szabadalmi jogokat a Kronski és Kröger, valamint a Heimsoeth és Rinke nevű, két, szintén berlini cég veszi meg.
A polgári üzleti életben kudarcot vallott gép a hadseregben (és a diplomáciában) szép karriert futott be. A Reichswehr rejtjelző osztálya már a 20-as évek közepén használja a gép „őskori” típusait, de az „igazi”, Enigma I néven 1935. június 27-én lép szolgálatba a Wehrmachtnál.
A polyák lehallgatók valami furcsa éteri hangra lett figyelmes 1927-ben. Ekkor már birtokukban volt a szabadalmi leírás és egy 1926-os üzleti célú típus. De ez más volt, okkal gyanították, hogy egy korai katonai célú gép. A hírszerzés Német Osztályának rejtjelző irodája a BS-4 (Biutro Szyfrow) parancsot kap, hogy nézzen utána. Még 1927-ben, a posnani egyetemmel összefogva,- titkos- kriptográfiai tanfolyam indul, 20 matematikussal, köztük Marian Reiewskivel, Jerzy Rózyczkival és Hennryk Zygalskival.
1929 januárjában a németek hibájából rájuk mosolyog a szerencse. 48 órára kezükbe kerül egy katonai Enigma. A Német Külügyi Hivatal a varsói nagykövetségük részére sima postai küldeményként egy gépet küld. Gondosan „szalmába csomagolva”, ahogy az akció egyik résztvevője Loicki ezredes megfogalmazta. Egy füles nyomán, pénteken a vámhivatal raktárából „kikölcsönzik” a gépet. Gondosan megvizsgálják, lefotózzák, majd ugyanolyan gondosan visszarakják a csomagolásába és visszaviszik a vámhivatalba. A németek nem sejtenek semmit. Az ezredes úgy fogalmazott, hogy bepillanthattak a 3 rejtjelző henger kapcsolatának és a további rejtjelzést szolgáló dugós csatlakozások összeköttetéseinek módozataiba. A 3 ásznak, - lengyel adatok szerint- 1932 decemberére sikerül megfejteniük az (akkori) Enigma rejtélyét. A BS-4 1934-ben, - szigorúan titkos- megbízást ad AVA Wytwornia Teletechnicznának (Varsó, Stepinska utca 25.), hogy építsen egy pontos másolatot. Reiewski a kódfejtést céljából 1938 novemberére megépíti a lengyel „Bombát”. A gépben levő megfejtőhengerek a 3 henger valamennyi betűkombinációján végigfutnak, a keresett helyzet megtalálásáig, amelynek a segítségével az AVA-Enigmával rejtjelzett szöveget lehet megfejteni.
Mivel ekkor már 1939 nyara van és szorít az idő, Stefan Mayer ezredes, a lengyel kémfőnök úgy dönt ideje megosztani az infókat az angolokkal és a franciákkal. Mayer és Gwido Langer, a rejtjelző iroda meghívására a 3 ország titkos konferenciát tart 1939. július 24-27. között a Wicher” nevű lengyel megfejtő központban, mely Varsótól 20 km-re, DNY-ra, a Pyry-i erdőben található. Francia részről Bertrand őrnagy, a rejtjelző iroda főnöke és Braquernié kapitány, kriptográfus, brit részről Denniston parancsnok az angliai „Goverment Code and Cipher School” főnöke, Knox, a főkriptogáfusa és egy oxfordi professzor van jelen. A vendégek elismerően csettintenek, és döntenek a jövőbeni együttműködésről. A lengyelek feladata továbbra is a matematikai-elméleti problémák megoldása, a briteké, hogy biztosítsák a napi kulcs megfejtését, a franciáké az ügynöké kapcsolatok fejlesztése.
A lengyelek 2 AVA változatot, a „Bomba” pauszpapírjait és egyéb kriptográfia anyagot küldenek repülővel, Skandinávián és Belgiumon át Párisba. Onnan Bertrand őrnagy 08.16.-án Londonba utazik, ahol Menzies ezredes, az MI6 főnöke veszi át tőle az anyagot. Szeptember 3-án megnyílik Bletchley.
2015.01.28. 09:45:37
Papírzsepi · http://lemil.blog.hu 2015.01.28. 09:49:36
Ellenben ha van kedved, írj róluk egy vendégposztot, szívesen felteszem. A téma simán kiadna egy jó posztot.
2015.01.28. 09:57:28
molnibalage · https://militavia.blog.hu/ 2015.01.28. 14:03:05
molnibalage · https://militavia.blog.hu/ 2015.01.28. 14:04:47
2015.01.28. 14:21:04
Minorkavidor 2015.01.28. 19:37:00
1914 novemberében döntő változás történt a Naval Inteligence Departement (NID) élén. Oliver tengernagyot, aki addig szolgálat élén állt vezérkari főnökké nevezték ki. William Reginald „Hunyori” Hall kapitány váltotta. A NID irodái „Room 40” néven vonulnak be a hírszerzés világtörténelmébe, a háború végén már 1.000 férfi és nő állt az alkalmazásában. Azonban a fontos desifrírozó osztályt előbb meg kell szervezni. Hallnak már az elején szerencséje van, találkozik Sir Alfred Ewinggel, aki mielőtt a haditengerészeti kiképzés vezetője lett volna, műegyetemen volt professzor, akinek hobbija a titkosírások megfejtése volt. Ewniget a német nyelv szakértőjeként Montgomery tiszteletes támogatja.
A Royal Navy ebben az időben 4 csoport lehallgató és bemérő állomást üzemeltet. 2 az „Admiralitás B” néven fut, 14-14 lehallgató és bemérő állomást, a másik 2 „X tengernagy” néven 8-8 állomást fog át. A RN 6 állomása a német flotta mozgását követi, készülékei olyan érzékenyek, hogy a hadihajók közti beszélgetéseket is veszik. A németek olyan könnyelműek, hogy sok üzenet kódolatlanul megy. Nemsokára napi 2.000 üzenettel dolgozhatnak.
A szerencse is melléjük áll. 1914.08.11-én, Richardson kapitány váratlanul rajta üt a Melburne-ben horgonyzó Hobart nevű német gőzösön. Minden hivatalos iratot elkoboz. Ezek között van a Handelsverkehrsbuch (HVB: a Kereskedelmi Forgalom Könyve), amit, - nevével ellentétben- a haditengerészet is használ. A HVB november végén Hall asztalán van.
Európában is szerencse kis éri őket. 1914.08.27-re virradóan a Magdeburg kiscirkáló, - a köd miatt – zátonyra fut a revali (Tallinn) támaszponttól kb. 50 tmf-re. Eredeti feladata, hogy a Finn-öbölben biztosítson egy elaknásító műveletet, visszaúton meg támadja és semmisítse meg az orosz előőrsöket és torpedórombolókat. Miután minden mentési kísérlet meghiúsul, a kapitány úgy dönt, hogy az orosz hadihajók megérkezése előtt minden iratot égessenek el a kazánban, kivéve a még használatban lévőket! Így megmarad 2 rejtjelkulcsokat tartalmazó könyv: 1 a hídon, 1 a rádiósszobában. Miután a kapitány parancsot ad a hajó elhagyására az egyik rádiós az előírásoknak megfelelően vízbe veti az egyik ólomnehezékkel ellátott könyvet, a másik könyv addigra eltűnt a rádiósszobából. A megérkező oroszok hadifogságba ejtik a legénységet. Majd álcázott akció keretében átkutatják a zátonyon ülő cirkálót és környezetét. Búváraik értékes kincseket találnak a tengerfenéken: az egyik kódkönyvet, térképeket, hajónaplót. Mivel Szentpéterváron úgy vélik, hogy e dokumentumokat Nagy-Britannia tudja a legjobban hasznosítani, így értesítik a briteket. 09.06-án Volnyikov az orosz hadtengerészeti attasé bejelentkezik Winston Churchillnél és bejelenti, hogy a cucc átvehető a Murmanszk melletti Alexandrovszkban (ma: Poljarnoje). A Theseus cirkáló 10.13-án érkezik vissza az ajándékkal. Ewingék rájönnek, hogy az üzenetek többségét 2x kódolják. Rotter hadnagy megtalálja a jelkulcsot is, melyről kiderül, hogy betűcserés eljáráson alapul.
Az évvégén 3. diadalukat ünneplik. Az történt, hogy Tirpitz elhatározta, hogy rombolók elaknásítják a Temze torkolatát. Az S115, S117, S118 és S117 jelű rombolók kifutnak, a brit egységek már várják őket. Előbb egy tengeralattjáró, majd 15h-kor 1 cirkáló és 4 romboló jelenik meg. Thiele korvettkapitány ekkor öngyilkos rohamra vezeti kötelékét, amely megsemmisül. Hiábavalóan, mert 11.30-án egy brit halászhajó a hollandiai Texel sziget közelében kihalászott tengerészládát ad le. A Kereskedelmi Könyvet találják benne. E könyv a tengeri és szárazföldi erők, a haditengerészeti attasék, konzulok, egyéb diplomaták és a gyarmati hatóságok közti üzenetek megfejtésére szolgál. 1914. december közepétől már napi részletességgel tudja tájékoztatni az Admiralitást a Kriegsmarine minden lépéséről.
A németek szánalmasan lassan reagálnak. Csak 1916-tól változtatják a kódokat, előbb havonta, majd naponta. A lényeg, a sifrírozó szisztéma viszont mindvégig azonos marad. London sokszor hamarabb értesül az üzenetről, mint maga az érintett.
L. B. Alberti 2015.01.28. 21:03:28
És még az én nézettségem is nőtt :) Külön köszönet érte!
GépBalta 2015.01.29. 01:11:37
Hírös Szögedi módszer.
2015.01.29. 08:57:10
noodlay 2015.01.29. 10:07:39
Némileg off-topic, de annál inkább on-blog gondolatok: egyrészt félelmetesnek tűnhet, hogy a modern háborúkban egy-egy matematikusnak nagyobb hatása van, mint egy egész gyalogos hadosztálynak, másrészt már a legkorábbi háborúk is technikai fejlődés melegágyai voltak. Van ebben a két képben némi mókás párhuzam: (1) diplomaták között egy matematikus magyarázza, miért lenne sokkal jobb az ő új titkosítási módszerét használni (2) Egri csillagok: Török Bálinték pisztollyal lövöldöznek az újonnan kapott páncélokra, és azt veszik meg, ami nem reped meg.
Mindkét esetben egy-egy technológiai újítás (újabb vasötvözet/matematika) fog a következő háborúban életet menteni - és megélhetést biztosítani a "technológiai szállítónak".
Minorkavidor 2015.01.29. 17:32:26
Ugyanis Perzsa-öböl menti állomáshelyéről,- ahol éveken át szolgált – Kairóba helyezték át. Adenben megtudja, hogy kitört a háború. Az internálástól tart, de tovább utazhat, kerülő utakon Berlinbe érkezik. A Kriegsmarine tartalékos tisztje, de a törökök jóvoltából mégsem a flottánál szolgál. ŐK ugyanis azt találták ki, hogy – semlegességük ellenére – titkos expedíciót szerveznek Afganisztánba angolellenes felforgatás céljából, ehhez német szakértőket keresnek. W. önként jelentkezik és a többi némettel együtt Konstantinápolyba küldik. Azonban nézeteltérések támadnak a törökökkel, amit megunván Wassmuss függetleníti magát, majd 14 decemberében útnak indul Bagdadba. Innen 15 januárjában a Pioneer nevű uszályt is vontató gőzösön lecsordogál a Tigrisen Szeib Sza ’ ad-ig, ami Bagdadtól 250 km-re fekszik. Ide a hó végére érkezik meg, hivatalosan Siraszba tart, hol átvegye konzuli tisztjét. Kíséretét 2 bagdadi német adja, Dr. Lenders orvos és a perzsául is jól beszélő Erik Bohnstorff, egy export-import cég képviselője.
A perzsa kormány kinyilvánította semlegességét, semlegességét, de a britek expedíciós sereggel megszállták az országot. A parancsok pol.-i tanácsadója Sir Percy Cox konzul jól ismerte W.-t még Busirból. Cox egyik bagdadi ügynökétől tudja, hogy W. Az országban van és ismeri megbízatásának céljait: rávenni a perzsa kormányt a KH melletti belépésre, fellázítani a britek ellen a sivatagi törzseket és az Anglo-Persian Oil Company Ltd. csővezetékeit elvágja. A RN innét szerezte be teljes olajalapú üzemanyag szükségletét. W. expedíciója a határátlépéstől számított 10 nap múlva eléri Diszfult. A település környékén lakó (főleg arab) törzseket) a britellenes dzsihád fűti, nagyszerű!
A csővezetéket hetekre megrongálják. Erre Cox egy angolbarát törzs néhány lovasát Sustárba küldi, ahol a német expedíciónak át kell haladnia. Mire a lovasok odaérnek a németek már tovább mentek, a Bahtár-kánok védelme alatt. Ez hidegzuhanyként éri Coxot, mert eddig úgy tudták, hogy barátaik, akikre,- igaz tekintélyes évi járadék fejében- rábízhatják a csővezeték védelmét. Az expedíció 03.02-án érte el Bonandzsant, mely 70 km-re van Busirtól. Pár nap múlva elérik a Bahtár-birtokok határát. Tadzs Maleki faluban már védelem nélkül éjszakáznak, itt rajtuk ütnek, néhány fegyveres körbevette a sátrukat. W. nem pánikol, a sötétség leple alatt elmenekül néhány csoki és kétszersült társaságában. Dr. Listermannál, az új busiri konzulnál akar menedéket keresni. Dr. Lenders elvonja az őr figyelmét, a többi őr aludt, így W.-nak sikerül a szökés. A doki ezalatt szétválogatja az expedíció legfontosabb iratait, így a kódkönyveket is. Majd némi baksis fejében rávette a csaverdárt, az öszvérhajcsárok vezetőjét, hogy rejtse el az övében, így azok meg is maradnak. A dokit és a poggyászt másnap átadják a briteknek. W. ellen hajtóvadászatot indítanak. W. a hajsza közben arról értesül, hogy egy brit kommandó, - a perzsa függetlenségre és a nemzetközi jogra fittyet hányva- lerohanta a busiri német konzulátust. Dr. Listermannt, a személyzet többi tagját és az iratokat egy brit hadihajóra vitték. Az iratok között volt a Német Külügyi Hivatal 13 040 számú diplomáciai kódmegfejtő könyve is. Ez a valós történet.
Hogy több publikációban más szerepel, az Hall tengernagy „Cover Story-jának” köszönhető. Mivel „Room 40” létezése titkot képzett, így kellett egy fedőtörténet, amely így hangzott:
1915 nyarának végén a már tengernagyi rangot viselő Hall találkozik egy betegszabadságát töltő tengerésztiszttel, aki a Perzsa-öbölben vívott harcokban sérült meg. (Hol is másutt)) A tiszt megemlíti W. menekülését, még azt is tudta, hogy nagyon mérges, mert elvesztette a csomagjait. (Minő tájékozottság ) ). Hall furcsállja, hogy miért ragaszkodik W. a csomagjai visszaadásához, ezért elküldi egyik segédtisztjét a raktárba ahol a busiri csomagokat őrizték. Eleinte reménytelen az ügy, oszt rájuk mosolyog a szerencse. Néhány hét múlva értesítik, hogy az iratok az Indian Office pincéjében pihennek (e részleg felelt a britek Perzsa-öböl-béli tevékenységéért). A hivatal nincs messze a ’Room 40” irodáitól. Az egyik felbontatlan (!) Csomagban megtalálják régóta keresett 13 040-es számú diplomáciai kódmegfejtő könyvet. (Hollywoodi Happy end) ).
A legenda valótlanságát az 1915-ben, Busirban alkonzulként tevékenykedő C. J. Edmuns 1916. évi jelentése is alátámasztja. E szerint W. szökése után az angol konzulátus elrendelte, hogy feltűnés nélkül vegyék őrizetbe a német konzulátus személyzetét. Listermann személyes holmija között „ több hosszú, gyapjú alsónadrágba bugyolálva két megfejtőkönyvet” találtak.
@Hadrian77:
Az ismert közmondás szerint a jó felderítés/hírszerzés fél győzelem!
2015.01.30. 08:23:03
wjozsi 2015.01.31. 14:48:12
teddybear01 2015.01.31. 18:39:50
Kár, hogy amint címlapos lett a bejegyzés, azonnal rászálltak a trollok.
paráznabillegető 2015.02.03. 11:39:17
OFF.
csak pár troll volt, és csak egyikük volt igazán kitartó. érdekes, nekem ő már az ingerküszöbömet alulról kapirgálta... kezdek keményedni, vagy érzéketlenedni, vagy mi...
mindegy, most ilyen világban élünk, kérem. de asszem mindig is ilyen volt ez, csak az üzenet közvetítésének eszköze változott, változik. anno prédikáltak, meg ugye a hordószónokok... ma blogerek és trollok...
hát igen.
ON.
MrR2008 2015.02.07. 22:38:31
2015.02.11. 22:28:25
@Hadrian77:
Szinten off:
2015. jan. 29.-en meghalt Stockholmban Stig Berling. Szokese utan Budapesten is elt.
intelnews.org/2015/02/09/01-1639/